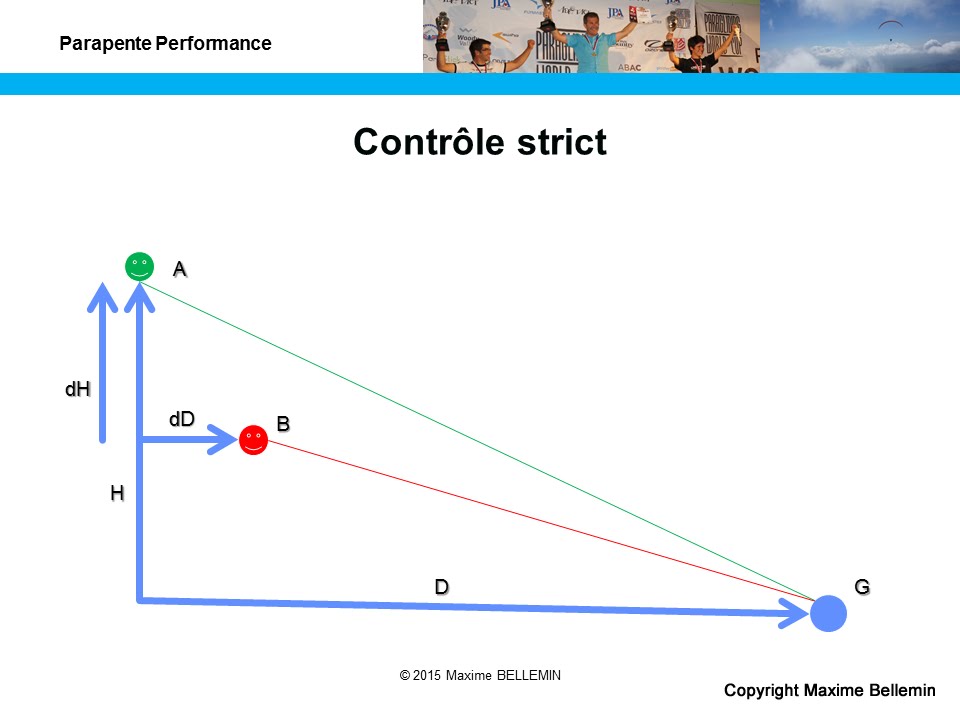
In this case, pilot A wishes to exercise a strict control over pilot B. He will fly faster than him to be sure to overtake his opponent before this guy has a chance to find a thermal. Pilot A is therefore seeking to catch pilot B further and lower on the course.
In theory
Our equations on glide ratios are the following:
-
- Fb = (D – dD) / (H – dH)
- Fa = D / H
By eliminating H:
- (1) dD = (1 – Fb / Fa) * D + Fb * dH
Our equations on time are the following:
-
- t = D / Va
- t = (D – dD) / Vb
By eliminating t:
- (2) D = dD * Va / (Va – Vb)
By eliminating D in between (1) and (2) and after various operations we reach the following:
- (3) Fc = (Va – Vb) / (Vza – Vzb)
We managed to find again the formula disclosed by Julien ! As a result the control glide ratio is the ratio of difference in horizontal speed to difference of sink rate between the two pilots.
As it will be difficult to perform mental arithmetic in flight, here is a handy chart giving control glide ratio from the input of pilots A and B transition speeds, calculations being based on the polar curve of a modern racing wing. You can spare the decimals as it is difficult enough to assess one full point of glide while flying.
We can determine also the range of the control exercised by pilot A over pilot B. By reinjecting dD in (2) we obtain the following:
- D = dH * Va / (Vza – Vzb)
In practice
Obviously this range depends on the difference in initial altitude between A and B. The faster the pilots fly, the shorter the range of control is. The more the pilot A wants to catch up quickly on pilot B, the more the range of its control decreases. Here are the distances obtained for an initial height differential of 100 m, depending on the horizontal speed adopted by A and B.
By construction of this modeling, pilot A has to travel a greater distance than pilot B during the same time. He is therefore forced to fly faster than his fellow pilot. Hence the white boxes in the tables. As soon as the conditions of the day lead to expect a Vzmc higher than 2 m/s, the flight speeds are quite fast. So that pilot A would have almost no chance to catch up and therefore have any control over any pilot B either in front of him who would always reach the G point by flying full speed.
Moreover our pilots seem to adopt speeds without any respect for the theories of MacCready. Pilot B is the one that should take it into account the most, but the equation does not mention that. The only thing that could preoccupy B in this configuration is to not touch the ground before A, and therefore to regulate his speed in order to have the glide ratio that allows reaching G point.
This occurs in a particular phase of the flight: the final glide. For the entire flight before this particular phase, our modeling and willingness to control are too strict. Also the estimate of the variables that make up the formula is particularly difficult. Let us prepare to go a step further by relaxing our control in the next episode.



Ping : The theory of "control" in paragliding developed by Maxime Bellemin