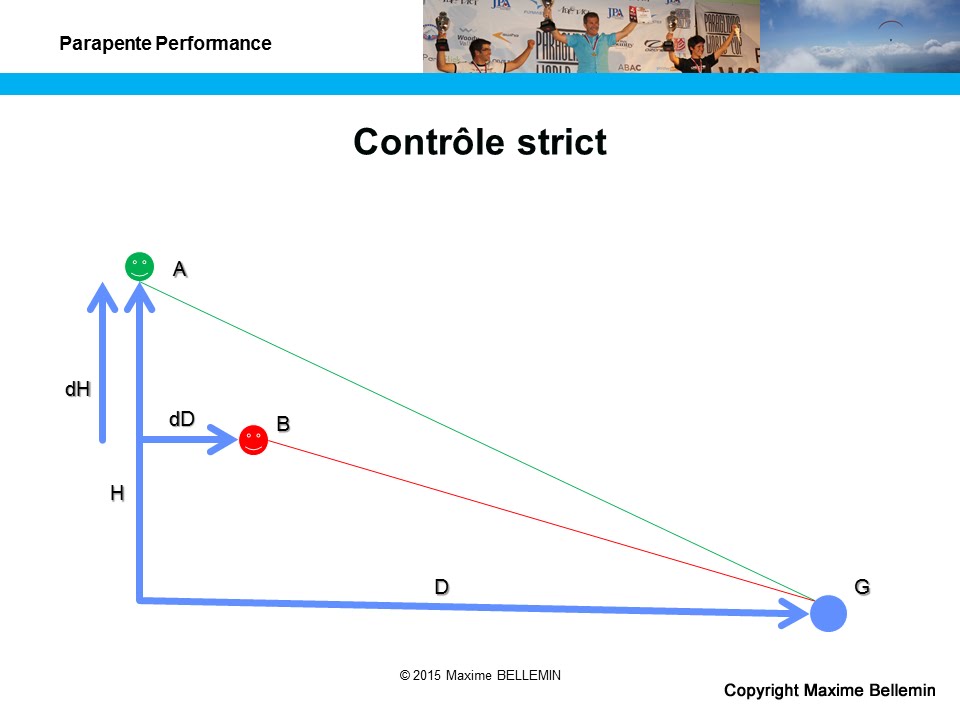
Dans ce cas, le pilote A souhaite exercer un contrôle strict sur le pilote B. Il va voler plus vite que lui pour être sûr de le chapeauter avant que son adversaire n’ait la moindre chance de trouver un thermique. Le pilote A cherche donc à rattraper le pilote B plus loin et plus bas sur le parcours.

Nos équations sur les finesses sont les suivantes:

• Fb = (D – dD) / (H – dH)

Fa = D / H

En éliminant H:

(1) dD = (1 – Fb / Fa) * D + Fb * dH

Nos équations sur le temps sont les suivantes :

• t = D / Va

t = (D – dD) / Vb

En éliminant t :

(2) D = dD * Va / (Va – Vb)

En éliminant D entre (1) et (2) et après diverses opérations nous arrivons à :

(3) Fc = (Va – Vb) / (Vza – Vzb)

Nous avons retrouvé la formule dévoilée par Julien! Il en résulte que la finesse de contrôle est le rapport du différentiel de vitesse au différentiel de taux de chute entre les deux pilotes.

Comme il vous sera bien difficile d’effectuer le calcul mental en vol, voici un tableau pratique donnant la finesse de contrôle qui résulte des vitesses en transition des pilotes A et B à partir de la polaire d’une aile de course. Je vous épargne les virgules, il est déjà suffisamment difficile d’évaluer en l’air un point de finesse pour ne pas tomber dans la découpe de suspente en 4.

Nous pouvons également déterminer la portée du contrôle de A sur B. En réinjectant dD dans (2) nous obtenons :

D = dH * Va / (Vza – Vzb)

Evidemment cette portée dépend de la différence d’altitude initiale entre A et B. Plus les pilotes volent vite, plus la portée du contrôle est réduite. Plus le pilote A veut rattraper B rapidement, plus la portée de son contrôle diminue. Voici les distances obtenues pour un différentiel d’altitude initial de 100 m, en fonction des vitesses adoptées par A et B.

Par construction dans cette modélisation, le pilote A doit parcourir une distance supérieure à B dans le même temps. Il est donc contraint de voler plus vite que son camarade. D’où les cases blanches dans les tableaux. Dès lors que les conditions du jour font espérer une Vzmc supérieure à 2 m/s le régime de vol est très rapide. Du coup A n’aurait presqu’aucune possibilité de rattraper et donc de contrôler quelque pilote B que ce soit devant lui qui atteindrait toujours le point G le premier en volant à toc.

Par ailleurs nos pilotes semblent adopter des vitesses sans le moindre respect pour les théories de MacCready. Le pilote B est celui qui devrait en tenir le plus compte, mais l’équation n’en fait pas mention. La seule chose qui pourrait préoccuper B dans cette configuration est de ne pas toucher le sol avant A, et donc de réguler sa vitesse pour avoir la finesse qui permet d’atteindre le point G.

Cette situation se produit dans une phase particulière du vol: le plané final. Pour tout le vol qui précède cette phase particulière, notre modélisation et notre volonté de contrôle sont trop stricts. De plus l’estimation des variables qui composent la formule est particulièrement ardue. Préparons-nous à aller un peu plus loin en relâchant notre contrôle dans le prochain épisode.